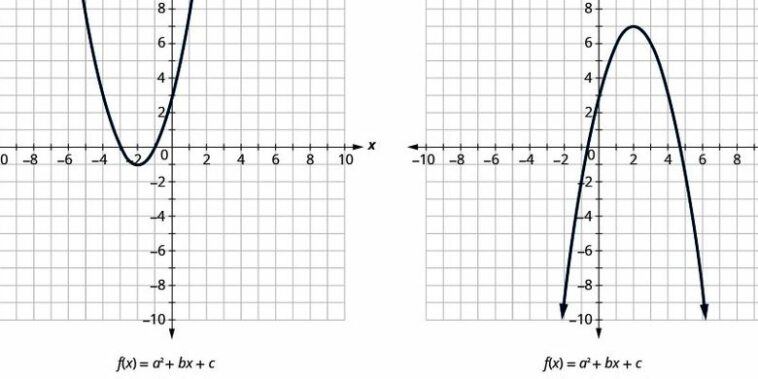
Fungsi kuadrat adalah bentuk umum dari suatu persamaan kuadratik, yaitu ax^2 + bx + c. Saat direpresentasikan dalam grafik, fungsi kuadrat menghasilkan kurva parabola yang memiliki sifat-sifat yang unik dan menarik untuk dipelajari.
Dalam artikel ini, kami akan membahas sifat fungsi kuadrat secara lengkap dan optimal. Kami akan meliputi beberapa topik yang penting dan memberikan wawasan yang bermanfaat untuk pemula dan ahli SEO.
Mengapa Sifat Fungsi Kuadrat Penting untuk Dipelajari?
Mempelajari sifat fungsi kuadrat sangat penting karena dapat membantu kita memahami banyak hal tentang kurva parabola. Sifat-sifatnya termasuk titik puncak, sumbu simetri, dan banyak lagi. Selain itu, sifat fungsi kuadrat juga membantu kita dalam menganalisis kasus-kasus khusus yang terjadi pada suatu kurva parabola.
Sebagai contoh, sifat fungsi kuadrat dapat digunakan dalam menghitung tinggi maksimum bola yang dilemparkan ke udara dan persamaan suhu bumi.
Titik Potong dengan Sumbu-y
Titik potong dengan sumbu-y menunjukkan di mana suatu persamaan kuadratik memotong sumbu-y atau sumbu vertikal ketika x adalah nol. Nilai y dari titik potong ini adalah nilai c pada persamaan kuadratik.
Jika kita memiliki persamaan kuadratik y = 2x^2 + 4x + 1, maka nilai c akan sama dengan 1. Oleh karena itu, titik potong dengan sumbu-y pada kurva tersebut adalah (0,1).
Titik Puncak
Titik puncak atau vertex adalah titik tertinggi atau terendah pada kurva parabola. Untuk menemukan titik puncak pada suatu kurva parabola, kita harus menemukan nilai x yang menjadi pusat simetri. Secara aljabar, kita dapat menggunakan rumus x = -b/2a untuk mencari pusat simetri.
Misalnya, pada persamaan kuadratik y = x^2 + 2x – 3, nilai a = 1 dan nilai b = 2. Kita dapat mencari nilai x dengan cara memasukkan nilai a dan b ke dalam rumus x = -b/2a. Hasilnya adalah -1, yang juga merupakan nilai x dari titik puncak.
Kita dapat menghitung nilai y dari persamaan kuadratik dengan memasukkan nilai x titik puncak yang telah kita temukan. Oleh karena itu, titik puncak pada kurva adalah (-1,-4).
Kebanyakan Fungsi Kuadratik Mempunyai Titik Puncak
Hampir semua fungsi kuadrat memiliki titik puncak. Namun, terdapat juga beberapa persamaan kuadratik yang tidak memiliki titik puncak, yaitu persamaan kuadratik yang konstan atau identik.
Persamaan kuadratik yang tidak memiliki titik puncak biasanya tidak membentuk kurva parabola. Alih-alih, kurva tersebut adalah garis lurus yang sejajar dengan sumbu-x.
Arah Bukaan Kurva Parabola
Arah bukaan kurva parabola menunjukkan apakah kurva membuka ke atas atau ke bawah. Kita dapat menentukan arah bukaan dengan melihat nilai a pada persamaan kuadratik.
Jika nilai a positif, maka kurva membuka ke atas. Jika nilai a negatif, maka kurva membuka ke bawah.
Simetri
Suatu kurva parabola memiliki sumbu simetri yang berupa garis lurus yang membagi kurva menjadi dua bagian simetris. Sumbu simetri selalu berada di antara titik puncak dan titik potong sumbu-x.
Untuk menentukan sumbu simetri, kita dapat menggunakan rumus x = -b/2a. Hasil dari rumus tersebut akan menjadi titik pusat simetri.
Kesimpulan
Mempelajari sifat fungsi kuadrat sangat penting untuk memahami dan menganalisis kurva parabola dengan lebih baik. Dalam artikel ini, telah dijelaskan beberapa sifat penting dari fungsi kuadrat, seperti titik potong dengan sumbu-y, titik puncak, arah bukaan, dan sumbu simetri.
Semoga artikel ini bermanfaat dan membantu Anda untuk memahami sifat fungsi kuadrat lebih baik. Jangan ragu untuk menghubungi kami jika Anda memiliki pertanyaan atau membutuhkan informasi lebih lanjut tentang topik ini.
FAQ
Q: Apakah setiap fungsi kuadratik memiliki titik puncak?
A: Hampir semua fungsi kuadrat memiliki titik puncak, kecuali persamaan kuadratik yang konstan atau identik.
Q: Bagaimana menentukan arah bukaan suatu kurva parabola?
A: Arah bukaan kurva parabola ditentukan oleh nilai a pada persamaan kuadratik. Jika nilai a positif, maka kurva membuka ke atas. Jika nilai a negatif, maka kurva membuka ke bawah.
Q: Apa yang dimaksud dengan sumbu simetri pada kurva parabola?
A: Sumbu simetri adalah garis lurus yang membagi kurva parabola menjadi dua bagian simetris. Sumu simetri selalu berada di antara titik puncak dan titik potong sumbu-x.