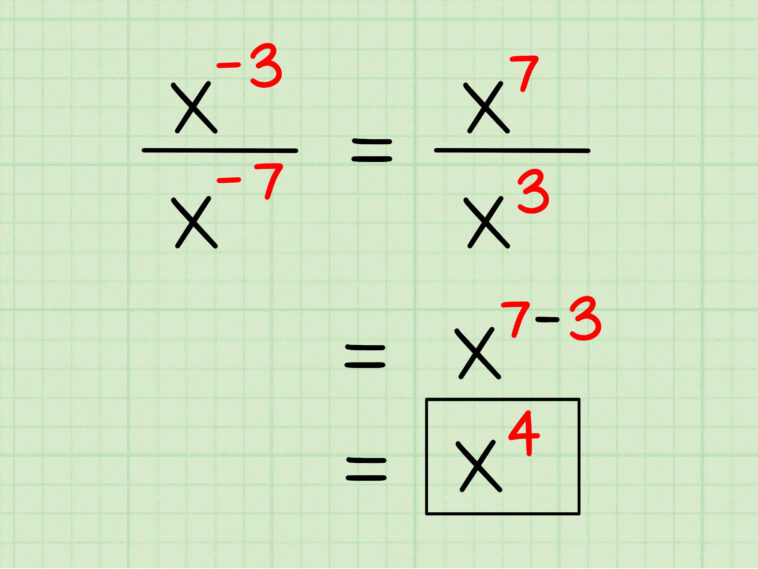
Pembagian perpangkatan adalah teknik matematika yang digunakan untuk memudahkan penghitungan pangkat bilangan pada operasi pembagian. Teknik ini sangat berguna dalam bidang ilmu pengetahuan, terutama di bidang matematika dan fisika. Artikel ini akan membahas secara komprehensif tentang pembagian perpangkatan, termasuk definisi, rumus, dan contohnya.
Definisi
Pembagian perpangkatan adalah teknik matematika yang digunakan untuk memudahkan penghitungan pangkat bilangan pada operasi pembagian. Dalam pembagian perpangkatan, bilangan yang dipangkatkan dibagi dengan bilangan pangkat lainnya untuk mendapatkan bilangan pemangkat. Sebagai contoh, dalam operasi 5^3 / 5^2, bilangan 5 ditiadakan dan yang tersisa yaitu 5^(3-2) = 5^1 = 5.
Rumus
Rumus yang digunakan dalam pembagian perpangkatan yaitu:
a^n / a^m = a^(n-m)
Dalam rumus tersebut, a merupakan bilangan yang dibagi, n adalah pangkat pertama, dan m adalah pangkat kedua.
Contoh:
3^7 / 3^4 = 3^(7-4) = 3^3 = 27
Contoh Pembagian Perpangkatan
Berikut adalah contoh penggunaan teknik pembagian perpangkatan dalam operasi matematika:
- 10^5 / 10^2 = 10^(5-2) = 10^3 = 1000
- 6^4 / 6^3 = 6^(4-3) = 6^1 = 6
- 2^6 / 2^4 = 2^(6-4) = 2^2 = 4
FAQ
Apa itu pembagian perpangkatan?
Pembagian perpangkatan adalah teknik matematika yang digunakan untuk memudahkan penghitungan pangkat bilangan pada operasi pembagian.
Mengapa penting menggunakan pembagian perpangkatan?
Pembagian perpangkatan sangat penting digunakan dalam bidang ilmu pengetahuan, terutama di bidang matematika dan fisika, karena teknik ini dapat memudahkan perhitungan dan menghemat waktu.
Bagaimana cara menggunakan pembagian perpangkatan?
Cara menggunakan pembagian perpangkatan yaitu dengan mengikuti rumus a^n / a^m = a^(n-m), di mana a merupakan bilangan yang dibagi, n adalah pangkat pertama, dan m adalah pangkat kedua.
Kesimpulan
Pembagian perpangkatan adalah teknik matematika yang sangat berguna dalam bidang ilmu pengetahuan, terutama di bidang matematika dan fisika. Dalam pembagian perpangkatan, bilangan yang dipangkatkan dibagi dengan bilangan pangkat lainnya untuk mendapatkan bilangan pemangkat. Teknik ini dapat memudahkan perhitungan dan menghemat waktu. Oleh karena itu, teknik pembagian perpangkatan harus dipelajari dan digunakan dalam operasi matematika secara efektif.