Pengantar
Dalam ilmu pengetahuan, terutama dalam matematika dan fisika, persamaan garis adalah salah satu konsep penting yang digunakan untuk mendeskripsikan hubungan antara dua variabel. Dalam artikel ini, kita akan menjelajahi dengan komprehensif dan optimal tentang cara menentukan persamaan garis. Jadi, jika Anda tertarik untuk mempelajari lebih lanjut, bacalah artikel ini sampai selesai!
Apa itu Persamaan Garis?
Secara sederhana, persamaan garis adalah metode untuk menggambarkan hubungan antara variabel-variabel tersebut dalam bentuk garis lurus pada sistem koordinat dua dimensi. Sebuah persamaan garis biasanya diwakili oleh bentuk umum y = mx + c, dimana y adalah variabel dependen, x adalah variabel independen, m adalah gradien garis, dan c adalah intercept pada sumbu y.
Cara Menentukan Persamaan Garis
Ada beberapa metode yang dapat digunakan untuk menentukan persamaan garis. Dalam artikel ini, kita akan membahas empat metode umum yang sering digunakan, yaitu metode titik-titik, metode garis tegak lurus, metode regresi linear, dan metode gradien-intercept.
1. Metode Titik-Titik
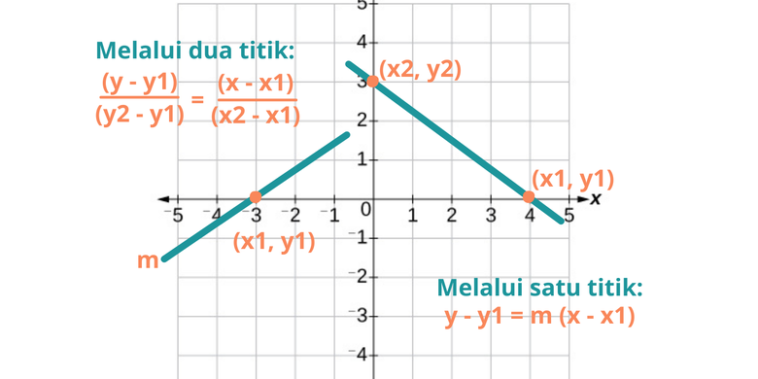
Metode ini melibatkan penggunaan dua titik pada garis untuk menentukan persamaannya. Dengan menggunakan rumus gradien (m) yang diberikan oleh (y2 – y1) / (x2 – x1), kita dapat menentukan nilai gradien. Kemudian, kita dapat menggunakan salah satu titik dan gradien untuk mencari intercept (c) menggunakan rumus y = mx + c.
- Tentukan dua titik yang berada pada garis.
- Hitung gradien menggunakan rumus (y2 – y1) / (x2 – x1).
- Gunakan salah satu titik dan gradien untuk mencari intercept dengan menggunakan rumus y = mx + c.
- Tuliskan persamaan garis dalam bentuk y = mx + c.
Poin-poin penting:
- Tentukan dua titik yang berada pada garis.
- Hitung gradien menggunakan rumus (y2 – y1) / (x2 – x1).
- Gunakan salah satu titik dan gradien untuk mencari intercept dengan menggunakan rumus y = mx + c.
- Tuliskan persamaan garis dalam bentuk y = mx + c.
2. Metode Garis Tegak Lurus
Metode ini melibatkan menggunakan dua garis yang tegak lurus satu sama lain untuk menentukan persamaan garis yang lain. Jika diketahui persamaan garis pertama, kita dapat menentukan gradien garis yang tegak lurus dengan memanfaatkan sifat garis-garis yang tegak lurus memiliki gradien yang saling berkebalikan dan hasil kali gradien adalah -1. Kemudian, kita dapat menggunakan titik yang diketahui pada garis yang tegak lurus untuk mencari intercept.
- Tentukan persamaan garis pertama.
- Gunakan sifat garis-garis tegak lurus untuk menentukan gradien.
- Gunakan titik yang diketahui untuk mencari intercept.
- Tuliskan persamaan garis tersebut.
Poin-poin penting:
- Tentukan persamaan garis pertama.
- Gunakan sifat garis-garis tegak lurus untuk menentukan gradien.
- Gunakan titik yang diketahui untuk mencari intercept.
- Tuliskan persamaan garis tersebut.
3. Metode Regresi Linear
Metode regresi linear melibatkan penggunaan data yang tersedia untuk menemukan persamaan garis terbaik yang menggambarkan hubungan antara dua variabel. Dalam metode ini, kita menggunakan teknik analisis statistik untuk menentukan persamaan garis yang paling mendekati data yang ada. Ini adalah metode yang paling umum digunakan dalam analisis data.
- Kumpulkan data yang relevan.
- Gunakan perangkat lunak analisis statistik untuk mencari persamaan garis terbaik.
- Analisis hasil dan interpretasikan persamaan garis.
Poin-poin penting:
- Kumpulkan data yang relevan.
- Gunakan perangkat lunak analisis statistik.
- Analisis hasil dan interpretasikan persamaan garis.
4. Metode Gradien-Intercept
Metode ini melibatkan penggunaan gradien dan intercept untuk menentukan persamaan garis. Jika diketahui gradien dan intercept pada sumbu y, kita dapat dengan mudah menentukan persamaan garis. Gradien (m) dapat diperoleh dari perubahan antara dua titik dan intercept (c) adalah titik pada sumbu y.
- Gunakan gradien dan intercept yang diketahui.
- Tuliskan persamaan garis dalam bentuk y = mx + c.
Poin-poin penting:
- Gunakan gradien dan intercept yang diketahui.
- Tuliskan persamaan garis dalam bentuk y = mx + c.
FAQ – Pertanyaan Umum
1. Apa itu persamaan garis?
Persamaan garis adalah metode penggambarkan hubungan antara dua variabel dalam bentuk garis lurus pada sistem koordinat.
2. Apa rumus untuk menghitung gradien garis?
Rumus gradien adalah (y2 – y1) / (x2 – x1).
3. Apa peran intercept dalam persamaan garis?
Intercept adalah titik tempat garis memotong sumbu y dalam persamaan yang ditentukan.
4. Apa metode yang umum digunakan untuk menentukan persamaan garis?
Metode yang umum digunakan adalah metode titik-titik, metode garis tegak lurus, metode regresi linear, dan metode gradien-intercept.
5. Apakah ada perangkat lunak khusus yang dapat digunakan untuk analisis regresi linear?
Ya, ada berbagai perangkat lunak analisis statistik yang tersedia untuk analisis regresi linear, seperti Minitab, SPSS, dan Python.
Kesimpulan
Secara keseluruhan, menentukan persamaan garis adalah proses penting dalam ilmu pengetahuan yang menggambarkan hubungan antara dua variabel. Dalam artikel ini, kita telah membahas empat metode umum yang sering digunakan untuk menentukan persamaan garis. Dengan memahami konsep ini, Anda dapat menerapkan metode yang tepat untuk data yang Anda miliki. Jadi, teruslah belajar dan praktikkan pengetahuan ini untuk meningkatkan pemahaman Anda tentang persamaan garis.