Hubungan Dua Sudut: Mengungkap Rahasia di Balik Geometri

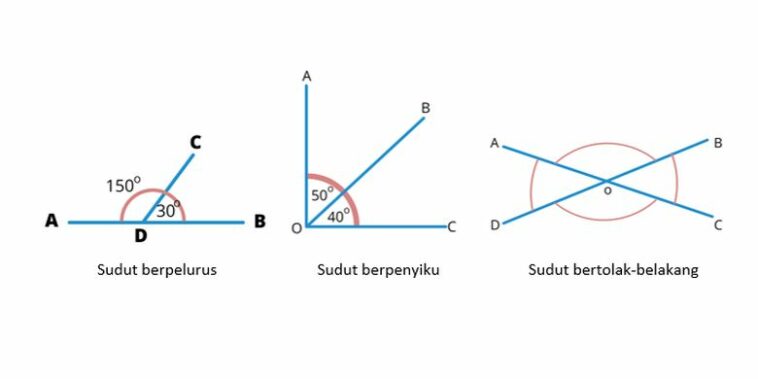
Judul: Menggali Lebih Dalam: Hubungan Dua Sudut dan Misteri di Baliknya

Suhu Kreativitas: 0,7

Hubungan dua sudut adalah konsep penting dalam matematika dan geometri yang sering digunakan dalam pemecahan berbagai masalah. Dalam artikel ini, kita akan menjelajahi secara komprehensif tentang hubungan dua sudut, mulai dari pengertian dasar, jenis-jenis hubungan, hingga penerapannya dalam kehidupan sehari-hari. Bersiaplah untuk dihadapkan pada wawasan yang berharga dan pengetahuan baru yang akan meramaikan pemahaman Anda tentang geometri!

Pendahuluan: Memahami Hubungan Dua Sudut

Pada dasarnya, hubungan dua sudut berkaitan dengan bagaimana sudut-sudut saling berinteraksi dan terkait satu sama lain. Dalam hal ini, kita dapat mengidentifikasi empat jenis hubungan utama antara dua sudut, yaitu: sudut komplementer, sudut suplemen, sudut beriringan, dan sudut berlawanan.

Sudut Komplementer

Sudut komplementer terjadi ketika dua sudut, saat digabungkan, membentuk sudut lurus 90 derajat. Contohnya, jika satu sudut memiliki ukuran 30 derajat, sudut komplementernya akan memiliki ukuran 60 derajat. Hubungan ini memainkan peran penting dalam pemecahan masalah yang melibatkan perbandingan sudut-sudut tertentu.

Poin penting:

• Sudut komplementer membentuk sudut lurus 90 derajat saat digabungkan.
• Ukuran sudut komplementer saling melengkapi satu sama lain.

Sudut Suplemen

Berbeda dengan sudut komplementer, sudut suplemen terjadi ketika dua sudut, saat digabungkan, membentuk sudut sejajar 180 derajat. Misalnya, jika satu sudut memiliki ukuran 60 derajat, sudut suplemen akan memiliki ukuran 120 derajat. Konsep ini sering digunakan dalam pembuktian geometri dan perhitungan sudut dalam bentuk-bentuk lainnya.

Poin penting:

• Sudut suplemen membentuk sudut sejajar 180 derajat saat digabungkan.
• Ukuran sudut suplemen saling melengkapi satu sama lain.

Sudut Beriringan

Sudut beriringan adalah dua sudut yang memiliki titik pangkal dan satu titik yang sama di antara keduanya. Sudut- sudut ini berada di sebelah-samping satu sama lain dan biasanya berbagi sisi yang sama. Hubungan ini membuka kemungkinan untuk mengkombinasikan hubungan-hubungan sudut lainnya dan memperluas aplikasinya dalam bentuk-bentuk geometri yang lebih kompleks.

Poin penting:

• Sudut beriringan berbagi titik pangkal dan satu titik di antara keduanya.
• Sudut beriringan berada di sebelah-samping satu sama lain.

Sudut Berlawanan

Sudut berlawanan adalah dua sudut yang ditempatkan di sisi yang berlawanan satu sama lain ketika dua garis sejajar saling memotong. Dalam kasus ini, kita dapat melihat bahwa sudut-sudut ini memiliki ukuran yang sama. Konsep ini sering digunakan dalam penentuan sudut yang berlawanan dalam memecahkan masalah geometri yang melibatkan pola-pola simetri dan sifat-sifat khusus dari suatu bentuk.

Poin penting:

• Sudut berlawanan memiliki ukuran yang sama.
• Sudut berlawanan terbentuk ketika dua garis sejajar saling memotong.

FAQ (Frequently Asked Questions)

1. Apa perbedaan antara sudut komplementer dan sudut suplemen?

   • Sudut komplementer membentuk sudut lurus 90 derajat saat digabungkan, sedangkan sudut suplemen membentuk sudut sejajar 180 derajat.

2. Apa yang dimaksud dengan sudut beriringan?

   • Sudut beriringan adalah dua sudut yang memiliki titik pangkal dan satu titik yang sama di antara keduanya.

3. Bagaimana sudut berlawanan dapat digunakan dalam geometri?

   • Sudut berlawanan digunakan untuk menentukan sudut yang berlawanan ketika dua garis sejajar saling memotong.

Kesimpulan

Dalam geometri, hubungan dua sudut adalah konsep penting. Sudut komplementer dan sudut suplemen membentuk sudut-sudut penting dalam perhitungan dan pembuktian matematis. Sudut beriringan dan sudut berlawanan memungkinkan kita untuk memahami interaksi sudut-sudut dalam konteks pola-pola simetri dan bentuk-bentuk geometri yang lebih kompleks. Dengan memahami konsep-konsep ini, kita dapat menerapkannya dalam pemecahan masalah dan meningkatkan pemahaman kita tentang geometri secara keseluruhan.

Pengetahuan tentang hubungan dua sudut memainkan peran penting dalam pemecahan masalah matematika dan memperkuat pemahaman kita tentang konsep-konsep geometri. Dengan memahami sudut komplementer, sudut suplemen, sudut beriringan, dan sudut berlawanan, kita dapat melihat hubungan kompleks di antara sudut-sudut yang merepresentasikan pola-pola dan struktur-sruktur yang kita temui dalam dunia nyata.

Mari kita terus belajar dan menjelajahi dunia geometri dengan pemahaman yang lebih mendalam tentang hubungan dua sudut!