Persamaan Linier 2 Variabel: Memahami Konsep dan Aplikasinya

Pendahuluan

Selamat datang dalam artikel ini yang akan mengajak Anda menjelajahi dunia persamaan linier 2 variabel. Dalam ilmu matematika, persamaan linier 2 variabel memiliki peranan yang sangat penting. Dalam artikel ini, kita akan membahas konsep dasar, aplikasi, dan pentingnya memahami persamaan linier 2 variabel. Siap untuk memulai?

Apa Itu Persamaan Linier 2 Variabel?

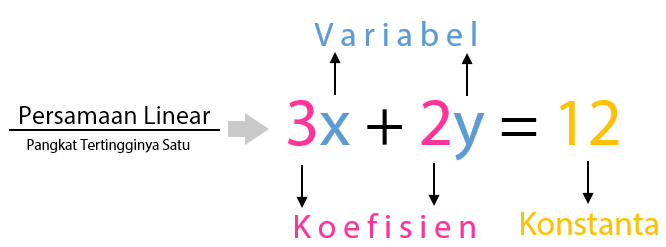
Persamaan linier 2 variabel adalah persamaan matematika yang mengandung dua variabel dan memiliki bentuk umum ax + by = c, di mana a, b, dan c adalah konstanta, sedangkan x dan y adalah variabel. Persamaan ini menunjukkan hubungan linier antara dua variabel dan bentuknya dapat bermacam-macam tergantung pada koefisien-koefisiennya.

Mengapa Persamaan Linier 2 Variabel Penting?

Persamaan linier 2 variabel sangat penting dalam matematika dan memiliki berbagai aplikasi di berbagai bidang. Beberapa alasan mengapa kita perlu memahami persamaan ini secara mendalam adalah sebagai berikut:

1. Ekonomi: Persamaan linier 2 variabel sering digunakan dalam model ekonomi untuk menganalisis hubungan antara dua variabel seperti pendapatan dan pengeluaran, harga dan jumlah penjualan, dan sebagainya.
2. Teknik: Dalam ilmu teknik, persamaan linier 2 variabel digunakan untuk memodelkan hubungan antara variabel-variabel seperti arus dan tegangan dalam rangkaian elektrik, kecepatan dan percepatan dalam mekanika, dan sebagainya.
3. Sains Alam: Dalam fisika, kimia, dan biologi, persamaan linier 2 variabel digunakan untuk menganalisis hubungan antara berbagai variabel seperti suhu dan tekanan, konsentrasi dan laju reaksi, dan sebagainya.
4. Statistik: Persamaan linier 2 variabel digunakan dalam analisis statistik untuk memodelkan hubungan antara dua variabel dalam bidang seperti regresi linier, korelasi, dan prediksi.

Bagaimana Cara Menyelesaikan Persamaan Linier 2 Variabel?

Untuk menyelesaikan persamaan linier 2 variabel, kita perlu mencari nilai-nilai variabel x dan y yang memenuhi persamaan tersebut. Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan linier 2 variabel, di antaranya adalah:

1. Metode Eliminasi: Metode ini melibatkan penghapusan salah satu variabel dari kedua persamaan, sehingga menghasilkan persamaan linier yang hanya mengandung satu variabel. Dengan menggantikan nilai variabel tersebut ke dalam persamaan lain, kita dapat menentukan nilai variabel yang lainnya.
2. Metode Substitusi: Metode ini melibatkan penggantian salah satu variabel dengan ekspresi yang mengandung variabel yang lain. Dengan memasukkan nilai ekspresi tersebut ke dalam persamaan lain, kita dapat menentukan nilai variabel yang lainnya.
3. Metode Matriks: Metode ini melibatkan mewakili persamaan linier 2 variabel dalam bentuk matriks dan menggunakan operasi aljabar matriks untuk menyelesaikan persamaan tersebut.

FAQ

1. Apa itu persamaan linier?

Persamaan linier adalah persamaan matematika yang mengandung variabel dengan pangkat paling tinggi adalah satu.

2. Mengapa penting untuk memahami persamaan linier 2 variabel?

Persamaan linier 2 variabel penting karena dapat digunakan untuk menganalisis hubungan antara dua variabel dalam berbagai bidang seperti ekonomi, teknik, dan sains alam.

3. Apa metode yang dapat digunakan untuk menyelesaikan persamaan linier 2 variabel?

Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan linier 2 variabel, di antaranya adalah metode eliminasi, metode substitusi, dan metode matriks.

4. Apa aplikasi dari persamaan linier 2 variabel?

Persamaan linier 2 variabel memiliki berbagai aplikasi, termasuk dalam bidang ekonomi, teknik, sains alam, dan statistik.

Kesimpulan

Persamaan linier 2 variabel merupakan konsep matematika yang penting dan memiliki banyak aplikasi di berbagai bidang. Dalam artikel ini, kita telah membahas konsep dasar, aplikasi, dan metode penyelesaian persamaan linier 2 variabel. Penting untuk memahami persamaan linier 2 variabel agar dapat menganalisis hubungan antara dua variabel dan mengambil keputusan yang tepat dalam berbagai situasi. Semoga artikel ini memberikan wawasan yang berharga kepada pembaca. Sekarang, saatnya untuk menerapkan pengetahuan ini dalam konteks nyata dan menggali lebih dalam tentang persamaan linier 2 variabel!