Pendahuluan
Dalam matematika, terdapat dua jenis deret yang sering ditemui yaitu deret aritmatika dan deret geometri. Deret aritmatika adalah deret bilangan dengan pola penambahan antar suku yang tetap, sedangkan deret geometri adalah deret bilangan dengan pola perkalian antar suku yang tetap.
Dalam artikel ini, kita akan membahas contoh-contoh soal seputar baris dan deret aritmatika dan geometri. Dengan pemahaman yang baik tentang konsep ini, kita dapat mengidentifikasi pola yang ada dalam suatu deret dan menyelesaikan soal-soal terkait dengan mudah.
Baris Aritmatika
Definisi
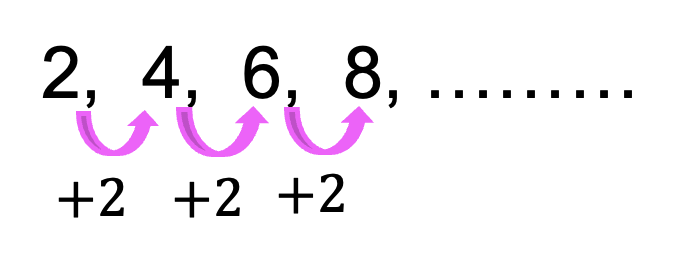
Baris aritmatika adalah barisan bilangan dimana setiap bilangan dihasilkan dengan menambahkan suku sebelumnya dengan suatu bilangan tetap yang disebut beda. Misalnya, jika suku pertama adalah a dan bedanya adalah d, maka suku kedua adalah a + d, suku ketiga adalah a + 2d, dan seterusnya.
Contoh Soal
- Diberikan baris aritmatika dengan suku pertama 2 dan beda 3. Berapakah suku ke-7 dalam baris ini?
- Jawab:
Untuk mencari suku ke-7, kita dapat menggunakan rumus umum untuk suku ke-n dalam baris aritmatika:
suku ke-n = suku pertama + (n-1) beda
Sehingga, suku ke-7 = 2 + (7-1) 3 = 2 + 6 * 3 = 2 + 18 = 20.
- Dalam suatu baris aritmatika, suku pertama adalah 5 dan suku kedua adalah 11. Berapakah beda dari baris ini?
- Jawab:
Untuk mencari beda, kita dapat menggunakan rumus umum untuk beda dalam baris aritmatika:
beda = suku kedua – suku pertama
Sehingga, beda = 11 – 5 = 6.
Kesimpulan
Baris aritmatika adalah barisan bilangan dengan pola penambahan antar suku yang tetap. Dalam menyelesaikan soal-soal terkait baris aritmatika, kita dapat menggunakan rumus umum untuk mencari suku ke-n dan beda.
Baris Geometri
Definisi
Baris geometri adalah barisan bilangan dimana setiap bilangan dihasilkan dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio. Misalnya, jika suku pertama adalah a dan rasionya adalah r, maka suku kedua adalah a r, suku ketiga adalah a r^2, dan seterusnya.
Contoh Soal
- Diberikan baris geometri dengan suku pertama 2 dan rasio 2. Berapakah suku ke-5 dalam baris ini?
- Jawab:
Untuk mencari suku ke-5, kita dapat menggunakan rumus umum untuk suku ke-n dalam baris geometri:
suku ke-n = suku pertama r^(n-1)
Sehingga, suku ke-5 = 2 2^(5-1) = 2 2^4 = 2 16 = 32.
- Dalam suatu baris geometri, suku pertama adalah 3 dan suku kedua adalah 6. Berapakah rasio dari baris ini?
- Jawab:
Untuk mencari rasio, kita dapat menggunakan rumus umum untuk rasio dalam baris geometri:
rasio = suku kedua / suku pertama
Sehingga, rasio = 6 / 3 = 2.
Kesimpulan
Baris geometri adalah barisan bilangan dengan pola perkalian antar suku yang tetap. Dalam menyelesaikan soal-soal terkait baris geometri, kita dapat menggunakan rumus umum untuk mencari suku ke-n dan rasio.
FAQ (Frequently Asked Questions)
Apa perbedaan antara baris aritmatika dan baris geometri?
Baris aritmatika memiliki pola penambahan antar suku yang tetap, sedangkan baris geometri memiliki pola perkalian antar suku yang tetap.
Apakah ada rumus umum untuk mencari suku ke-n dalam baris aritmatika dan geometri?
Ya, untuk baris aritmatika, rumusnya adalah suku ke-n = suku pertama + (n-1) beda. Sedangkan untuk baris geometri, rumusnya adalah suku ke-n = suku pertama r^(n-1).
Bagaimana cara mencari beda dalam baris aritmatika dan rasio dalam baris geometri?
Dalam baris aritmatika, beda dapat dicari dengan rumus beda = suku kedua – suku pertama. Sedangkan dalam baris geometri, rasio dapat dicari dengan rumus rasio = suku kedua / suku pertama.
Kesimpulan
Dalam artikel ini, kita telah membahas tentang contoh soal baris dan deret aritmatika dan geometri. Kedua jenis deret ini memiliki pola yang dapat diidentifikasi dan digunakan untuk menyelesaikan soal-soal terkait dengan mudah.
Penting untuk memahami rumus umum yang digunakan dalam mencari suku ke-n, beda, dan rasio dalam kedua jenis deret ini. Dalam menjawab soal-soal terkait baris aritmatika dan geometri, kita dapat menggunakan rumus-rumus tersebut untuk mendapatkan jawaban yang akurat.
Dengan pemahaman yang baik tentang baris dan deret aritmatika dan geometri, kita dapat meningkatkan kemampuan dalam matematika dan mengaplikasikan konsep ini dalam situasi yang lebih kompleks. Tetaplah berlatih dan terus mencoba soal-soal baru untuk mengasah kemampuan dalam memahami dan menyelesaikan masalah terkait dengan baris dan deret ini.