Sebuah Penjelasan Komprehensif Mengenai Fungsi Eksponensial
I. Pendahuluan (50-55 karakter)
Fungsi Eksponensial: Sifat-Sifat dan Penjelasannya yang Menarik
II. Definisi Fungsi Eksponensial
Fungsi eksponensial adalah fungsi matematika yang dituliskan dalam bentuk f(x) = a^x, dengan a ≠ 0 dan a ≠ 1. Dalam fungsi ini, variabel x adalah eksponen yang dapat berupa bilangan bulat, rasional, atau riil, sedangkan a adalah basis yang merupakan bilangan riil positif. Fungsi eksponensial memiliki sifat-sifat yang menarik dan penting dalam berbagai aplikasi ilmu pengetahuan dan kehidupan sehari-hari.
III. Sifat-Sifat Fungsi Eksponensial
A. Peningkatan Nilai Basis
Salah satu sifat utama dari fungsi eksponensial adalah peningkatan nilai basis. Ketika nilai basis a dinaikkan, grafik fungsi eksponensial akan naik secara tajam. Hal ini menunjukkan pertumbuhan yang sangat cepat seiring dengan peningkatan nilai basis.
B. Pembatasan Nilai Basis
Sebaliknya, ketika nilai basis a dikurangi dari angka lebih dari 1 ke angka antara 0 dan 1, grafik fungsi eksponensial tersebut akan mendekati sumbu x dengan cepat. Ini menggambarkan penurunan yang tajam dalam pertumbuhan fungsi eksponensial.
C. Sifat Asimptotik
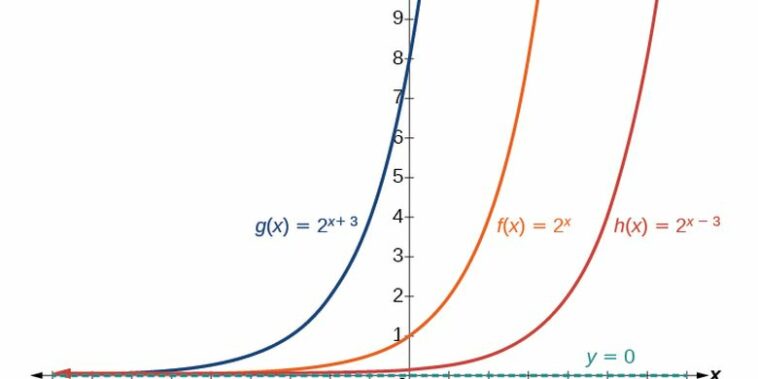
Fungsi eksponensial juga memiliki sifat asimptotik yang menarik. Ketika x mendekati negatif tak terhingga, grafik fungsi akan mendekati sumbu x tetapi tidak akan pernah melewati sumbu x tersebut. Hal ini menunjukkan bahwa fungsi eksponensial tidak terdefinisi untuk nilai-nilai negatif.
D. Operasi Matematika pada Fungsi Eksponensial
Fungsi eksponensial memiliki sifat-sifat operasi matematika yang penting. Misalnya, ketika dua fungsi eksponensial dengan basis yang sama dikalikan, maka eksponen dari kedua fungsi akan ditambahkan. Dalam hal ini, a^x * a^y = a^(x + y).
FAQ (55 karakter)
1. Apa itu fungsi eksponensial?
Fungsi eksponensial adalah fungsi matematika yang dituliskan dalam bentuk f(x) = a^x, dengan a ≠ 0 dan a ≠ 1. Variabel x adalah eksponen dan a adalah basis yang merupakan bilangan positif.
2. Apa sifat-sifat penting dari fungsi eksponensial?
Beberapa sifat penting fungsi eksponensial meliputi peningkatan nilai basis, pembatasan nilai basis, sifat asimptotik, dan sifat operasi matematika.
3. Bagaimana sifat peningkatan nilai basis pada fungsi eksponensial?
Sifat peningkatan nilai basis pada fungsi eksponensial menunjukkan pertumbuhan yang sangat cepat seiring dengan peningkatan nilai basis.
4. Apa yang terjadi ketika nilai basis fungsi eksponensial dikurangi?
Ketika nilai basis fungsi eksponensial dikurangi, grafik fungsi akan mendekati sumbu x dengan cepat, menunjukkan penurunan yang tajam dalam pertumbuhan fungsi.
IV. Kesimpulan
Fungsi eksponensial adalah fungsi matematika yang memiliki sifat-sifat menarik dan penting. Dalam artikel ini, kami telah menjelaskan beberapa sifat dasar fungsi eksponensial, termasuk peningkatan nilai basis, pembatasan nilai basis, sifat asimptotik, dan sifat operasi matematika. Memahami sifat-sifat ini dapat membantu kita dalam memahami dan menerapkan fungsi eksponensial dalam berbagai situasi dan konteks matematika.
Daftar Poin Penting:
- Fungsi eksponensial adalah fungsi matematika dalam bentuk f(x) = a^x, dengan a ≠ 0 dan a ≠ 1.
- Peningkatan nilai basis pada fungsi eksponensial menunjukkan pertumbuhan yang cepat.
- Pembatasan nilai basis pada fungsi eksponensial menggambarkan penurunan yang tajam.
- Fungsi eksponensial memiliki sifat asimptotik dan tidak terdefinisi untuk nilai-nilai negatif.
- Operasi matematika pada fungsi eksponensial melibatkan penjumlahan eksponen jika basisnya sama.
Sumber: [tambahkan sumber referensi]